Fractions Quizzes
Fractions Practice for GCSE Maths Foundation – Simplify, Add, Subtract, Multiply & Divide
Difficulty: Foundation
Curriculum: GCSE
Start QuizFractions Questions for GCSE Higher Tier Maths – Simplify, Add, Subtract, Multiply, Divide
Difficulty: Higher
Curriculum: GCSE
Start Quiz
Visual overview of Fractions.
Fractions – GCSE Maths Explained with Examples
Understanding fractions is one of the most important foundations in GCSE Maths. Fractions appear in exam questions, real-life problems, and topics such as percentages, ratios, and algebra. Learning how to add, subtract, multiply, and divide fractions accurately will help you gain confidence and improve your overall grade.
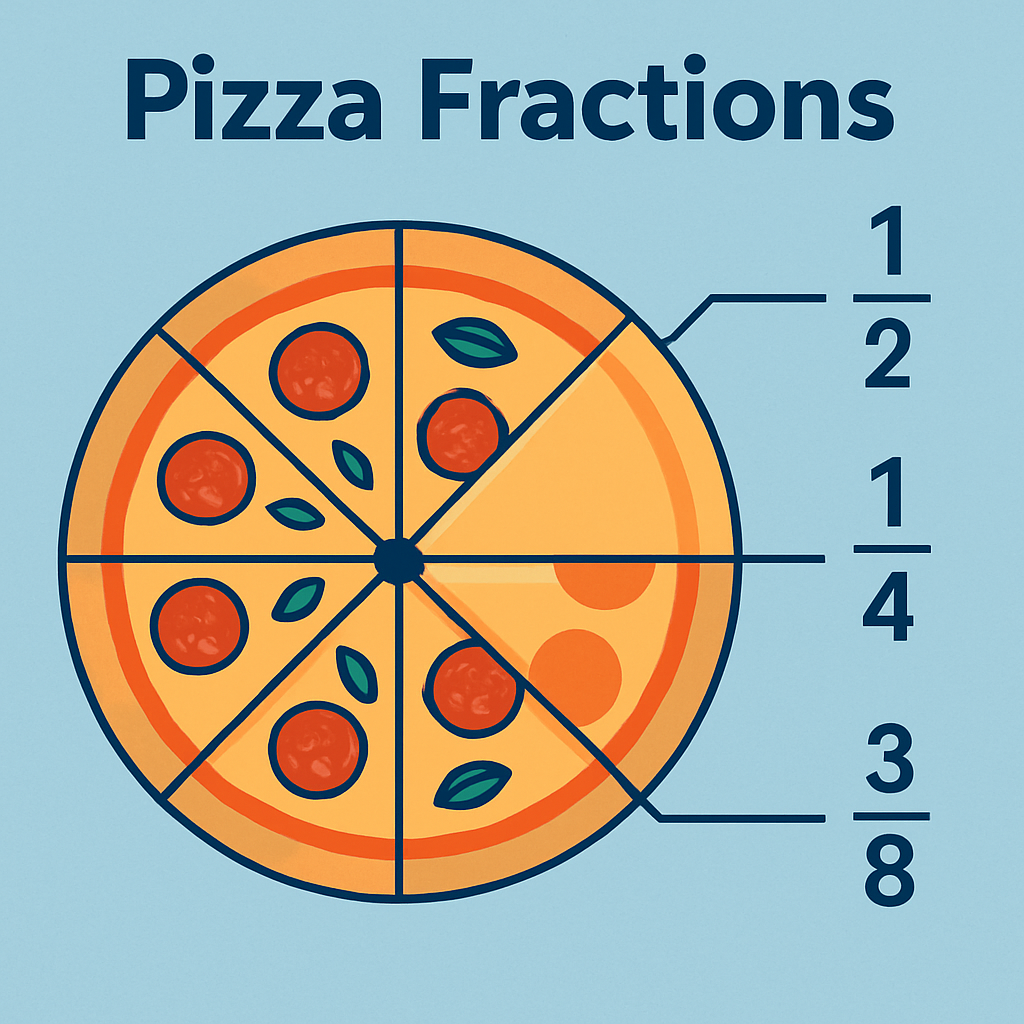
Fractions represent equal parts of a whole — like slices of a pizza.
What is a Fraction?
A fraction represents part of a whole. It is written as a/b, where:
- a is the numerator – the number of parts you have
- b is the denominator – the total number of equal parts
Example: \( \frac{3}{4} \) means three parts out of four equal parts.

Types of Fractions
- Proper fractions: Numerator is less than denominator (e.g. \( \frac{2}{5} \))
- Improper fractions: Numerator ≥ denominator (e.g. \( \frac{7}{4} \))
- Mixed numbers: Whole number and proper fraction (e.g. \( 1 \frac{3}{4} \))
- Equivalent fractions: Different fractions with the same value (e.g. \( \frac{1}{2} = \frac{2}{4} \))
How to Work with Fractions
1️⃣ Adding and Subtracting Fractions
- Find a common denominator.
- Add or subtract the numerators only.
- Keep the denominator the same.
- Simplify if possible.
Example: \( \frac{1}{4} + \frac{2}{4} = \frac{3}{4} \)
2️⃣ Multiplying Fractions
- Multiply numerators together.
- Multiply denominators together.
- Simplify the result.
Example: \( \frac{2}{3} \times \frac{3}{5} = \frac{6}{15} = \frac{2}{5} \)
3️⃣ Dividing Fractions
- Flip the second fraction (take its reciprocal).
- Multiply the first by the reciprocal.
- Simplify your final answer.
Example: \( \frac{2}{3} \div \frac{4}{5} = \frac{2}{3} \times \frac{5}{4} = \frac{10}{12} = \frac{5}{6} \)

Worked Examples
Example 1 – Foundation
Add \( \frac{1}{2} + \frac{1}{3} \):
- LCM of 2 and 3 → 6
- \( \frac{1}{2} = \frac{3}{6} \), \( \frac{1}{3} = \frac{2}{6} \)
- Add numerators → \( 3 + 2 = 5 \)
- Answer: \( \frac{5}{6} \)
Example 2 – Higher
Subtract \( \frac{7}{4} - \frac{5}{6} \):
- LCM of 4 and 6 → 12
- \( \frac{7}{4} = \frac{21}{12} \), \( \frac{5}{6} = \frac{10}{12} \)
- \( 21 - 10 = 11 \)
- Answer: \( \frac{11}{12} \)
Example 3 – Multiplication
\( \frac{3}{5} \times \frac{2}{7} = \frac{6}{35} \)
Example 4 – Division
\( \frac{5}{8} \div \frac{2}{3} = \frac{5}{8} \times \frac{3}{2} = \frac{15}{16} \)
Common Mistakes
- Forgetting to find a common denominator before adding/subtracting.
- Not simplifying the final result.
- Mixing numerator and denominator positions.
- Forgetting to flip the second fraction during division.
Real-Life Applications
- Cooking: measuring \( \frac{1}{2} \) cup or \( \frac{3}{4} \) teaspoon
- Shopping: calculating \( \frac{1}{4} \) discounts or deals
- DIY projects: measuring \( \frac{3}{5} \) of a length
- Algebra: simplifying fractional coefficients

Tips for Exams
- Memorise common fractions and their decimal equivalents.
- Write working clearly — fractions often carry 2–3 marks each in GCSE exams.
- Always reduce to simplest form to get full marks.
- Double-check by converting to decimals to see if the answer makes sense.
Summary
Fractions are the foundation for higher maths topics like algebra, percentages, and ratios.
The key to mastering them is practice and repetition.
Try the interactive Fraction Quizzes
Step 1: Find the lowest common denominator (LCD) of 2 and 3 → 6. Step 2: Convert: \( \frac{1}{2}=\frac{3}{6} \), \( \frac{1}{3}=\frac{2}{6} \). Step 3: Add numerators: \( 3+2=5 \). Keep denominator 6. Answer: \( \frac{5}{6} \) (already in simplest form). Step 1: LCD of 4 and 6 → 12. Step 2: Convert: \( \frac{7}{4}=\frac{21}{12} \), \( \frac{5}{6}=\frac{10}{12} \). Step 3: Subtract numerators: \( 21-10=11 \). Keep denominator 12. Answer: \( \frac{11}{12} \) (cannot be simplified further). Step 1: Multiply numerators: \( 3 \times 2 = 6 \). Step 2: Multiply denominators: \( 5 \times 7 = 35 \). Step 3: Simplify if possible: \( \frac{6}{35} \) has no common factors → already simplest. Answer: \( \frac{6}{35} \). Step 1: Keep–Change–Flip: \( \frac{5}{8} \times \frac{3}{2} \). Step 2: Multiply: numerators \( 5 \times 3 = 15 \), denominators \( 8 \times 2 = 16 \). Step 3: Simplify: \( \frac{15}{16} \) is already simplest. Answer: \( \frac{15}{16} \).Worked Solutions
Solution — Example 1 (Foundation): \( \frac{1}{2} + \frac{1}{3} \)
Solution — Example 2 (Higher): \( \frac{7}{4} - \frac{5}{6} \)
Solution — Example 3 (Multiplication): \( \frac{3}{5} \times \frac{2}{7} \)
Solution — Example 4 (Division): \( \frac{5}{8} \div \frac{2}{3} \)