Angles Quizzes
Visual overview of Angles.
Introduction
Angles are everywhere: from the corners of a room to the turns in a road. Understanding angles helps you solve geometry problems, make sense of real-world designs, and prepare for GCSE Maths exams. Mastery of angles builds the foundation for triangles, polygons, parallel lines, and trigonometry, and is key to confident problem-solving.
Core Concepts
What is an Angle?
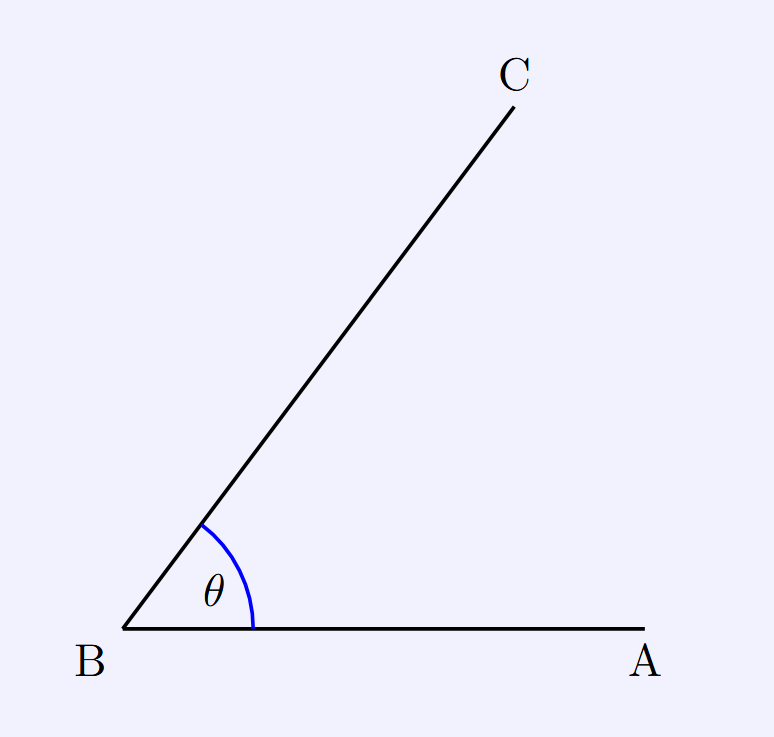
An angle is formed when two straight lines meet at a point, called the vertex. The amount of turn between the two lines is measured in degrees (°).
Examples: A right angle is 90°, a straight angle is 180°, and a full turn is 360°.
Types of Angles
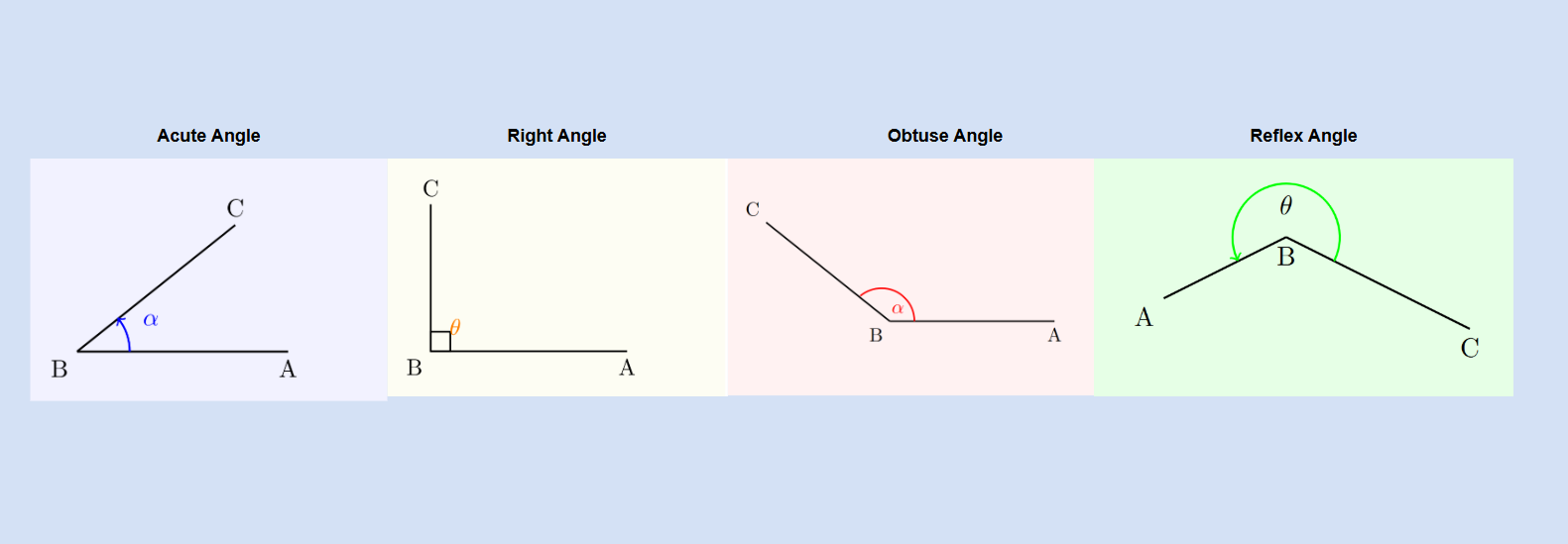
- Acute angle: less than 90°
- Right angle: exactly 90°
- Obtuse angle: between 90° and 180°
- Straight angle: exactly 180°
- Reflex angle: between 180° and 360°
- Full turn: exactly 360°
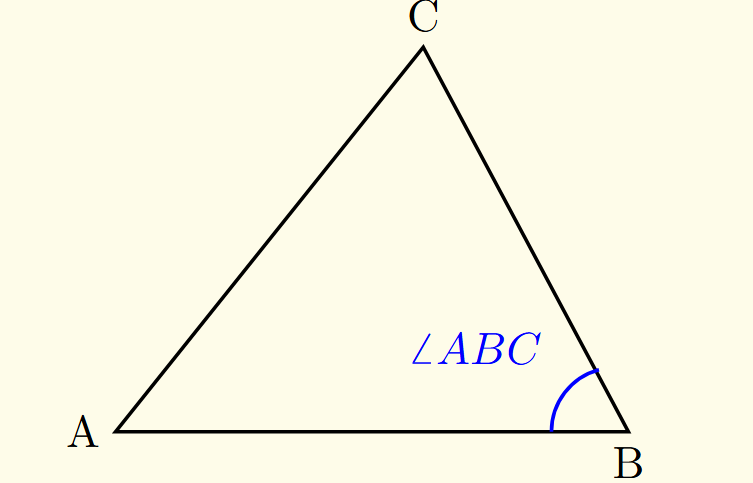
Angle Notation
- Angles are denoted as ∠ABC, with the vertex at B.
- Sometimes simply written as x° or θ.
Rules & Steps
- Straight line: sum of angles = 180° → ∠A + ∠B = 180°
- Around a point: sum of angles = 360° → ∠A + ∠B + ∠C + ∠D = 360°
- Vertically opposite angles: angles opposite each other are equal → x = y
- Triangle angles: sum of interior angles = 180° → ∠A + ∠B + ∠C = 180°
- Quadrilateral angles: sum of interior angles = 360° → ∠A + ∠B + ∠C + ∠D = 360°
- Parallel lines (transversal):
- Corresponding angles are equal
- Alternate interior angles are equal
- Co-interior angles sum to 180°
- n-sided polygon: sum of interior angles = (n-2) × 180°, each interior angle in a regular polygon = ((n-2) × 180)/n
Worked Examples
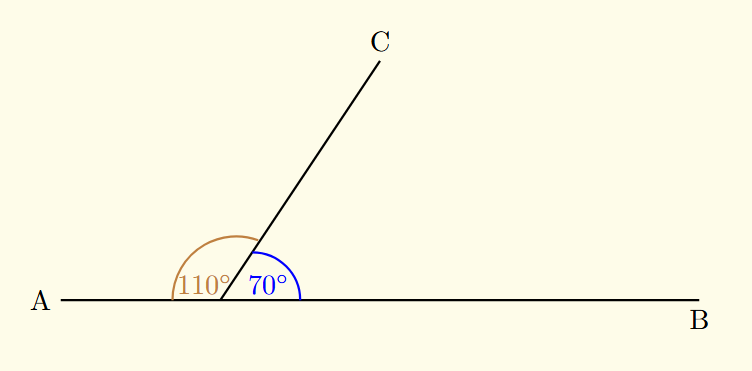
Straight line
Known: ∠A = 70°
Rule: Angles on a straight line sum to 180°
Calculation: ∠B = 180 - 70 = 110°
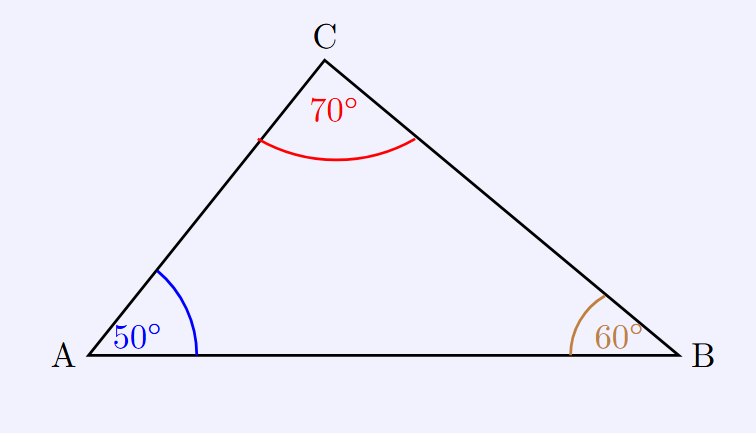
Triangle
Known: ∠A = 50°, ∠B = 60°
Rule: Sum of interior angles = 180°
Calculation: ∠C = 180 - (50 + 60) = 70°
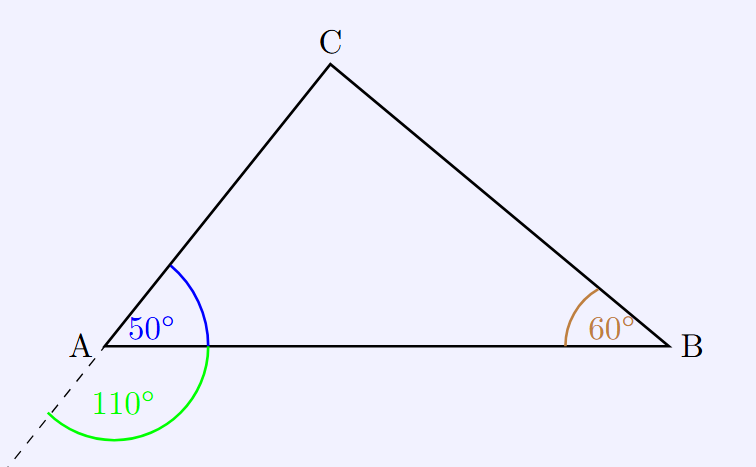
Exterior angle of a triangle
Opposite interior angles = 50° + 60° → exterior angle = 110°
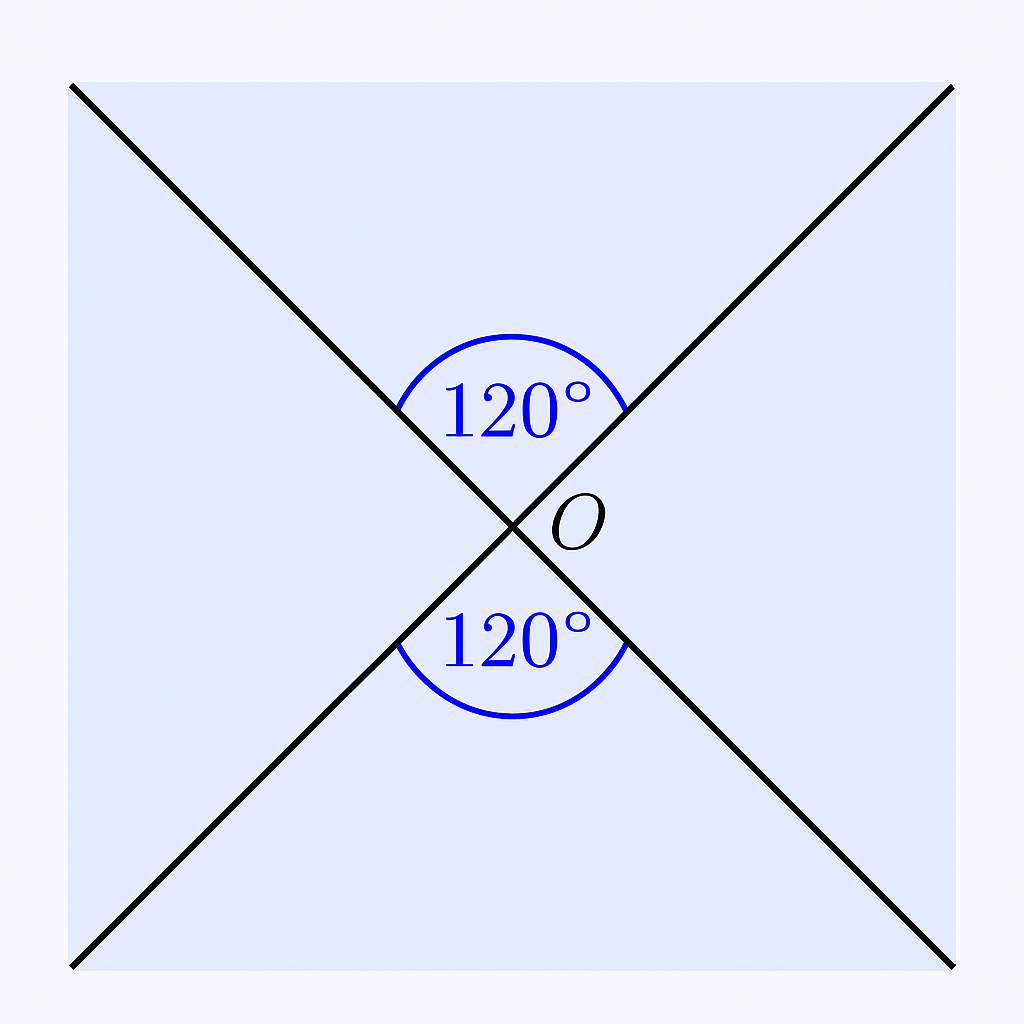
Vertically opposite angles
One angle = 120°, opposite angle = 120°
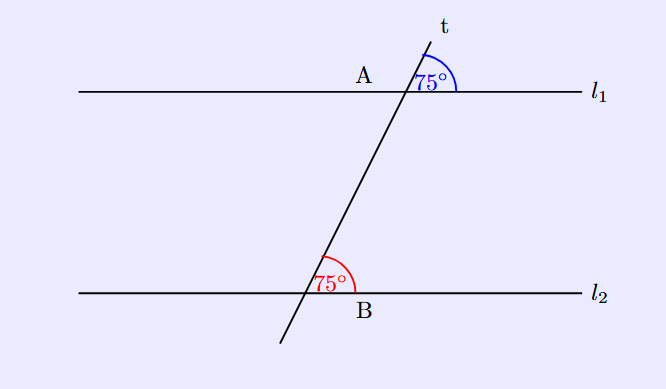
Parallel lines
One corresponding angle = 75°, the other = 75°
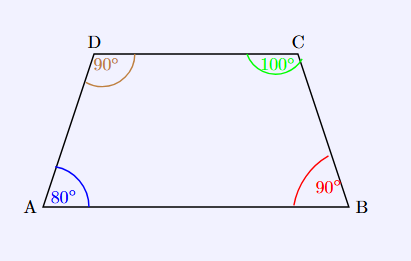
Quadrilateral
Given angles = 80°, 90°, 100°
Calculate fourth: 360 - (80 + 90 + 100) = 90°
Polygon
Regular hexagon interior angles: (6-2) × 180 / 6 = 120°

Common Mistakes
- Forgetting triangle angles sum to 180°
- Mixing up alternate and corresponding angles
- Confusing interior and exterior angles
- Not checking polygon sums before calculating individual angles
- Arithmetic errors when solving for unknown angles
Applications
- Architecture: designing safe and aesthetic structures
- Engineering: calculating forces and mechanics angles
- Navigation: bearings and course plotting
- Design & Art: creating tiling patterns and computer graphics
Strategies & Tips
- Label diagrams clearly: known in blue, unknown in red
- Apply angle rules systematically: straight line, point, triangle, quadrilateral
- Check sums in polygons before calculating individual angles
- Use parallel line rules carefully, double-check with diagrams
- Practice visualizing angles and drawing accurate diagrams
- Mnemonic: STRAIGHT → Straight = 180°, Triangle = 180°
Summary
Angles are central to GCSE Maths. Understanding types, relationships, and rules for triangles, quadrilaterals, polygons, and parallel lines allows students to solve diverse problems accurately. Regular practice, accurate diagram labeling, and systematic application of rules build confidence and exam readiness. Attempt the quizzes and exercises to consolidate your knowledge and improve your problem-solving skills.